Answer:
The thinness of film is 116 nm.
Step-by-step explanation:
Given that,
Wavelength = 650 nm
Refractive index = 1.40
We need to calculate the thickness
Using formula of thickness for destructive interference
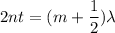
Here, m = 0
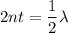
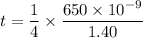

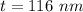
Hence, The thinness of film is 116 nm.