Question

The perimeter of a sector of a circle is the sum of the two sides formed by the radii and the length of the included arc. A sector of a particular circle has a perimeter of 28 cm and an area of 49 sq cm. What is the length of the arc of this sector?

Answer 1

Length of the arc of this sector, l = 14 cm

Step-by-step explanation:

It is given that, the perimeter of a sector of a circle is the sum of the two sides formed by the radii and the length of the included arc.

Perimeter of sector, P = 28 cm

Area of sector,
`A=49\ cm^2`

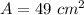
According to figure,

2r + l = 28 ............(1)

Area of sector,
`A=(\theta)/(360)* \pi r^2`

Where,
`\theta` is in radian and
`\theta=(l)/(r)`

Since,
`1^(\circ)=(\pi)/(180)\ radian`

`A=(l)/(2\pi r)* \pi r^2`

`r=(98)/(l)`

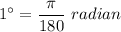
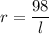
Put the value of r in equation (1) so,

`2* ((98)/(l))+l=28`

`l^2-28l+196=0`

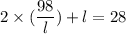
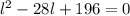
On solving above equation for l we get, l = 14 cm. So, the length of the arc of this sector is 14 cm. Hence, this is the required solution.