Question

Light rays in a material with index of refraction 1.31 can undergo total internal reflection when they strike the interface with another material at a critical angle of incidence. Find this material\'s index of refraction when the required critical angle is 78.3°.

Answer 1

The refractive index of the material is 1.28.

Step-by-step explanation:

It is given that,

Refractive index of medium 1, n₁ = 1.31

Critical angle,
`\theta_c=78.3`

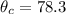
At critical angle rays will reflects at 90 degrees. Using Snell's law as:

`n_1sin\theta_1=n_2sin\theta_2`

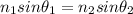
At critical angle,
`n_1sin\ \theta_c=n_2\ sin90`

`n_1sin\ \theta_c=n_2`

`n_2=1.31* sin(78.3)`

`n_2=1.28`

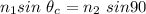
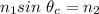
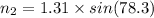
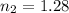
So, the refractive index of the material is 1.28. Hence, this is the required solution.