Question

A gas sample containing 1.94 moles at 25°C exerts a pressure of 450. torr. Some gas is added to the same container and the temperature is increased to 40.°C. If the pressure increases to 750. torr, how many moles of gas were added to the container? Assume a constant-volume container.

Answer 1

3.078 moles

Step-by-step explanation:

Given:

Number of moles of gas, n = 1.94 moles

Initial temperature, T₁ = 25° C = 298 K

Initial pressure, P₁ = 450 torr

Final temperature, T₂ = 40° C = 313 K

Final pressure, P₂ = 750 torr

now,

we know

PV = nRT

where,

P is the pressure

V is the volume

n is the number of moles

R is the universal gas constant

T is the temperature

now for the initial stage, the above relation comes as:

450 × V = 1.94 × R × 298 .............(1)

for the final stage

750 × V = n × R × 313 ............... (2)

on dividing the equation 2 by 1 we get

`(750)/(450)=(n*313)/(1.94*298)`

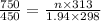
or

n = 3.078 moles

Answer 2

Answer : The number of moles of gas added to the container were, 3.078 mole

Explanation :

Using ideal gas equation,

`PV=nRT`

At constant volume the formula will be,

`(P_1)/(P_2)=(n_1* T_1)/(n_2* T_2)`

where,

`n_1` = initial moles of gas = 1.94 moles

`n_2` = final moles of gas = ?

`P_1` = initial pressure of gas = 450 torr

`P_2` = final pressure of gas = 750 torr

`T_1` = initial temperature of gas =
`25^oC=273+25=298K`

`T_2` = final temperature of gas =
`40^oC=273+40=313K`

Now put all the given values in the above formula, we get:

`(450torr)/(750torr)=(1.94mole* 298K)/(n_2* 313K)`

`n_2=3.078mole`

Therefore, the number of moles of gas added to the container were, 3.078 mole