Question

A box with an open top will be constructed from a rectangular piece of cardboard. The piece of cardboard is 10 inches wide and 14 inches long. The box will be constructed by cutting out equal squares of side x at each corner and then folding up the sides. What is the appropriate domain for the function V(x) that gives the volume of the box as a function of x?

Answer 1

Domain of the function is { x : x∈R, x>0 } or (0,∞).

Explanation:

It is given that the dimensions of a rectangular piece of cardboard are

Length = 14 inch

Width = 10 inch

The box will be constructed by cutting out equal squares of side x at each corner and then folding up the sides. So the dimensions of the box are

Length = 14-2x inch

Breadth = 10- 2x inch

Height = x inch

The volume of cuboid box is

`V=length* breadth * height`

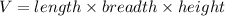
The volume function of the box is

`V=(14-2x)* (10-2x)* x`

`V=(14-2x)(10-2x)x`

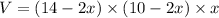
The volume function is V=(14-2x)(10-2x)x.

It is a polynomial function and domain of a polynomial function is all real numbers.

Here, x represents the height of the box. So, value of x must be a positive real number.

Domain of the function is

Domain = { x : x∈R, x>0 }

It can be written as (0,∞).

Therefore, domain of the function is { x : x∈R, x>0 } or (0,∞).