Question

What would be the volume of (a) air (b) plastic in a ball with 25cm diameter made from plastic 2mm thick?

Answer 1

Volume of air is
`7797918.85 mm^3` and volume of plastic is
`386604.9523 mm^3`

Explanation:

Diameter of ball = 25 cm = 250 mm

Radius of ball =
`(250)/(2)=125 mm`

Outer radius R = 125 mm

Thickness = 2mm

Inner radius r = 125-2 = 123 mm

Ball is in the shape of sphere =
`(4)/(3) \pi r^3`

For volume of air inside the ball we will consider the inner radius

Volume of air =
`(4)/(3) \pi r^3`

=
`(4)/(3) * (22)/(7) * 123^3`

=
`7797918.85 mm^3`

Volume of plastic = Outer volume - Inner Volume

=
`(4)/(3) \pi R^3 - (4)/(3) \pi r^3`

=
`(4)/(3) \pi (R^3 - r^3)`

=
`(4)/(3) * (22)/(7)(125^3 - 123^3)`

=
`386604.9523 mm^3`

Hence Volume of air is
`7797918.85 mm^3` and volume of plastic is
`386604.9523 mm^3`

Answer 2

Part a) The volume of the air is
`V=7,794.78\ cm^(3)`

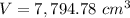
Part b) The volume of the plastic is
`V=386.45\ cm^(3)`

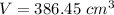
Explanation:

we know that

The volume of the sphere is equal to

`V=(4)/(3)\pi r^(3)`

step 1

Find the volume of the complete ball (air +plastic)

we have

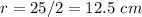`r=25/2=12.5\ cm` ------> the radius is half the diameter

substitute

`V=(4)/(3)\pi (12.5)^(3)`

`V=8,181.23\ cm^(3)`

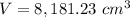
step 2

Find the volume of the air

we have that

The plastic is 2 mm thick

Convert to cm

2 mm=2/10=0.2 cm

so

The radius of the interior of the ball is

`r=12.5-0.2=12.3\ cm`

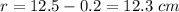
substitute

`V=(4)/(3)\pi (12.3)^(3)`

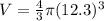
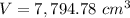`V=7,794.78\ cm^(3)` -----> this is the volume of the air (interior of the ball)

step 3

Find the volume of the plastic

we know that

The volume of the plastic is equal to the volume of the complete ball minus the volume of the air

so

`8,181.23\ cm^(3)-7,794.78\ cm^(3)=386.45\ cm^(3)`