Question

A soft drink machine outputs a mean of 27 ounces per cup. The machine's output is normally distributed with a standard deviation of 3 ounces. What is the probability of filling a cup between 21 and 28 ounces? Round your answer to four decimal places.

Answer 1

Answer: 0.6065

Explanation:

Given : The machine's output is normally distributed with

`\mu=27\text{ ounces per cup}`

`\sigma=3\text{ ounces per cup}`

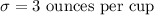
Let x be the random variable that represents the output of machine .

z-score :
`z=(x-\mu)/(\sigma)`

For x= 21 ounces

`z=(21-27)/(3)\approx-2`

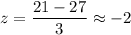
For x= 28 ounces

`z=(28-27)/(3)\approx0.33`

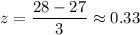
Using the standard normal distribution table , we have

The p-value :
`P(21<x<28)=P(-2<z<0.33)`

`P(z<0.33)-P(z<-2)=0.6293-0.0227501=0.6065499\approx0.6065`

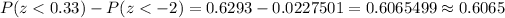
Hence, the probability of filling a cup between 21 and 28 ounces= 0.6065