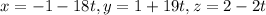Answer:
Explanation:
We are given that
Equation of paraboloid
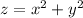

And equation of the ellipsoid
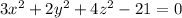
We have to find the parametric equation for tangent line to the curve of the intersection of the paraboloid and ellipsoid at point (-1,1,2).
We have to find the normal at point (-1,1,2)
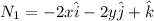
Normal at point (-1,1,2)
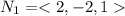
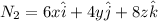
Normal at point (-1,1,2)
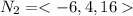
We rescale and set

The tangent vector to the curve of intersection is given by
 =
=
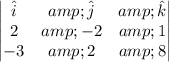
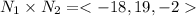
Hence, the tangent line is given by