Question

SOMEONE PLEASE HELP TODAY!!!! The cross-sectional areas of a right triangular prism and a right cylinder are congruent. The right triangular prism has a height of 6 units, and the right cylinder has a height of 4 units. Which conclusion can be made from the given information?

The volume of the triangular prism is half the volume of the cylinder.

The volume of the triangular prism is twice the volume of the cylinder.

The volume of the triangular prism is equal to the volume of the cylinder.

The volume of the triangular prism is not equal to the volume of the cylinder.

Answer 1

The volume of the triangular prism is not equal to the volume of the cylinder.

Explanation:

we know that

The cross-sectional areas of a right triangular prism and a right cylinder are congruent

That means-----> The area of the triangular base of triangular prism is equal to the area of the circular base of the cylinder

step 1

Find the volume of triangular prism

The volume of triangular prism is equal to

`V=BH`

where

B is the area of the triangular base

H is the height of the prism

we have

`H=6\ units`

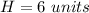
substitute

`Vp=B(6)`

`Vp=6B\ units^3`

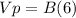
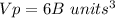
step 2

Find the volume of cylinder

The volume of the cylinder is equal to

`V=BH`

where

B is the area of the circular base

H is the height of the cylinder

we have

`H=4\ units`

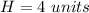
substitute

`Vc=B(4)`

`Vc=4B\ units^3`

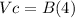
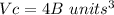
step 3

Compare the volumes

`(Vp)/(Vc)=(6B)/(4B)`

simplify

`(Vp)/(Vc)=(3)/(2)=1.5`

so

`Vp=1.5Vc`

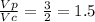
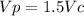
so

The volume of the prism is 1.5 times the volume of the cylinder

therefore

The volume of the triangular prism is not equal to the volume of the cylinder.