We're looking for
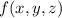 such that
such that
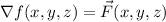 , which requires
, which requires
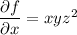
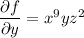
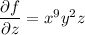
Integrating both sides of the first PDE wrt
 gives
gives
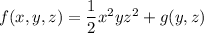
Differenting this wrt
 gives
gives
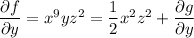
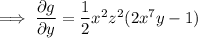
but we're assuming
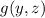 is a function that doesn't depend on
is a function that doesn't depend on
 , which is contradicted by this result, and so there is no such
, which is contradicted by this result, and so there is no such
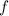 and
and
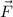 is not conservative.
is not conservative.