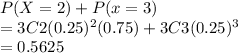Answer:
Explanation:
Given that for a three-question multiple-choice pop quiz, a student is totally unprepared and randomly guesses the answer to each question. Each question has four answer choices. With guessing, the response on one question is not influenced by the response on another question. Thus, whether one question is answered correctly is independent of whether or not another question is answered correctly. Let C denote the event the student selects the correct answer for any given question and I denote the event the student selects the incorrect answer for any given question.
Since there are four answer choices and one is correct
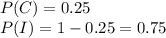
Let X be the number of questions answered correctly.
Then X is Bin (3,0.25)
Prob student passes, answering at least two questions correctly
=
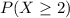
=