Question

Discrete Components, Inc., manufactures a line of electrical resistors. Presently, the carbon composition line is producing 100 ohm resistors. The population variance of these resistors "must not exceed 4" to conform to industry standards. Periodically, the quality control inspectors check for conformity by randomly selecting 10 resistors from the line and calculating the sample variance. The last sample had a variance of 4.36. If the critical value of chi-square is 16.919 and the observed value is 15.247, the appropriate decision is to _____.

Answer 1

Answer with explanation:

Claim : The population variance of these resistors "must not exceed 4" to conform to industry standards.

Then , the set of the hypothesis will be :-

`H_0: \sigma\leq4`

`H_a: \sigma>4`

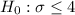
The critical value of chi-square is 16.919 and the observed value is 15.247 .

We know that if the chi-square observed value is less than the chi-square critical value, then we fail to reject the null hypothesis.

Since 15.247<16.919

So , we conclude that we do not reject the null hypothesis.

Hence, we have enough evidence to support the claim that the population variance of these resistors "must not exceed 4" to conform to industry standards.