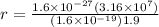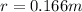Answer:
Part a)
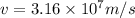
Part b)
r = 0.166 m
Step-by-step explanation:
Part a)
As we know that the energy of the Hydride ion is given as
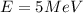
here we have
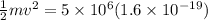
also we know that

now we have

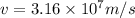
Part b)
As we know that magnetic force on the charge is centripetal force
so we have

so we have
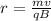
so we have