Question

A tablet of a common over-the-counter drug contains 2.00 x 102 mg of caffeine (C8H10N4O2; molar mass = 194.0 g/mol). What is the pH of the solution resulting from the dissolution of two of these tablets in 225. mL of water at 25oC? (For caffeine, Kb = 4.1 x 10-4.)2.766.337.6710.9611.24

Answer 1

pH of the solution is 11.24

Step-by-step explanation:

Total mass of caffeine in 225 mL solution upon dissolution of two tablets =
`(2* 2.00* 10^(2))mg=(2* 2.00* 10^(2)* 10^(-3))g=0.4g`

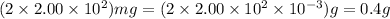
So molarity of caffeine in solution =
`(0.4* 1000)/(225* 194)M=0.00916M`

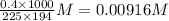
We have to construct an ice table to calculate change in concentration at equilibrium

`C_(8)H_(10)N_(4)O_(2)+H_(2)O\rightleftharpoons HC_(8)H_(10)N_(4)O_(2)^(+)+OH^(-)`

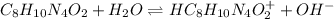
I:0.00916 0 0

C:-x +x +x

E:0.00916-x x x

So,
`([HC_(8)H_(10)N_(4)O_(2)^(+)][OH^(-)])/([C_(8)H_(10)N_(4)O_(2)])=K_(b)`

Species inside third bracket represent equilibrium concentrations

So,
`(x^(2))/(0.00916-x)=0.00041`

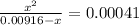
or,
`x^(2)+0.00041x-(3.76* 10^(-6))=0`

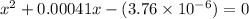
Hence
`x=\frac{-0.00041+\sqrt{(0.00041)^(2)+(4* 3.76* 10^(-6))}}{2}`

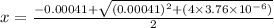
So,
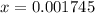`x=0.001745`M

So,
`pH=14-pOH=14+log[OH^(-)]=14+logx=14+log(0.001745)=11.24`