Question

Fine grains of beach sand are assumed to be spheres of radius 64.8 µm. These grains are made of silicon dioxide which has a density of 2600 kg/m3 . What is the mass of each grain of sand? Answer in units of kg. 013 (part 2 of 2) 1.0 points Consider a cube whose sides are 0.514 m long. How many kg of sand would it take for the total surface area of all the grains of sand to equal the surface area of the cube? Answer in units of kg.

Answer 1

1) Mass of the grain is
`2.9632* 10^(-9) kg`.

2) 0.08901 kg of sand would have surface area equal the surface area of the cube.

Step-by-step explanation:

1) Radius of the grain,r = 64.8 µm =
`6.48* 10^(-5)m`

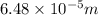
Volume of the sphere =
`(4)/(3)\pi r^3`

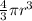
Volume of the grain of a sand:

`V=(4)/(3)* \pi r^3=(4)/(3)* 3.14* (6.48* 10^(-5) m)^3`

`V=1.1397* 10^(-12) m^3`

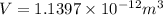
Density of a grain of sand =
`d=2600 kg/m^3`

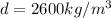
Mass of a grain of a sand = M

`d=2600 kg/m^3=(M)/(1.1397* 10^(-12) m^3)`

`M=2.9632* 10^(-9) kg`

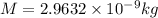
Mass of the grain is
`2.9632* 10^(-9) kg`.

2) Surface are of sphere:
`4\pi r^2`

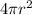
Surface area of a grain:

`A=4* 3.14* (6.48* 10^(-5)m)^2`

`A=5.2766* 10^(-8) m^2`

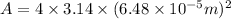
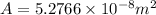
Length of the cube = a = 0.514 m

Total surface area of cube ,A'=
`6a^2`

`A'=6* (0.514 m)^2=1.5851 m^2`

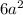
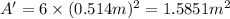
let the number grains with area equal to total surface area of cube be x.

`A'=A* x`

`x=(1.5851 m^2)/(5.2766* 10^(-8) m^2)=3.003* 10^7`

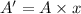
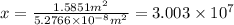
Volume of x number of grains :V'

`V'=V* x`

`V= 1.1397* 10^(-12) m^3* 3.003* 10^7`

`V'=3.4236* 10^(-5) m^3`

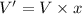
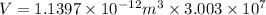
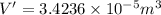
Mass of
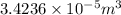`3.4236* 10^(-5) m^3` of sandL:

=
`3.4236* 10^(-5) m^3* 2600 kg/m^3=0.08901 kg`

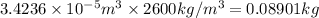
0.08901 kg of sand would have surface area equal the surface area of the cube.