Answer:
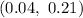
Explanation:
The confidence interval for population proportion is given by :-
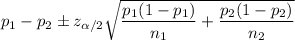
Given : Significance level :
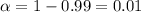
Critical value :
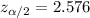
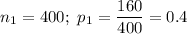
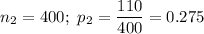
Then a 99% confidence interval is constructed to estimate the difference in population proportions which possess the given characteristic will be :-
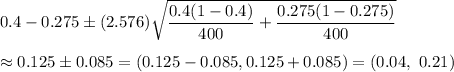
Hence, the resulting confidence interval is
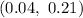 .
.