Question

A quality-conscious disk manufacturer wishes to know the fraction of disks his company makes which are defective. Step 2 of 2 : Suppose a sample of 815 floppy disks is drawn. Of these disks, 701 were not defective. Using the data, construct the 90% confidence interval for the population proportion of disks which are defective. Round your answers to three decimal places.

Answer 1

Answer: (0.120,0.160)

Explanation:

Given : Sample size :
`n=815`

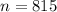
Number of disks were not defective =701

Then , the number of disks which are defective =
`815-701=114`

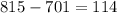
Now, the proportion of disks which are defective :
`p=(114)/(815)\approx0.14`

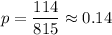
Significance level :
`\alpha: 1-0.9=0.1`

Critical value :
`z_(\alpha/2)=1.645`

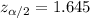
The confidence interval for population proportion is given by :-

`p\pm\ z_(\alpha/2)\sqrt{(p(1-p))/(n)}\\\\=0.14\pm(1.645)\sqrt{((0.14)(1-0.14))/(815)}\\\\\approx0.14\pm0.020=(0.14-0.020,0.14+0.020)=(0.120,0.160)`

Hence, the 90% confidence interval for the population proportion of disks which are defective = (0.120,0.160)