Question

A railroad car of mass 2.00 3 104 kg moving at 3.00 m/s collides and couples with two coupled railroad cars, each of the same mass as the single car and moving in the same direction at 1.20 m/s. (a) What is the speed of the three coupled cars after the collision

Answer 1

3 milliseconds

Step-by-step explanation:

Answer 2

Given:

Mass of the rail road car, m = 2 kg

velocity of the three cars coupled system, v' = 1.20 m/s

velocity of first car,
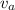`v_(a)` = 3 m/s

Solution:

a) Momentum of a body of mass 'm' and velocity 'v' is given by:

p = mv

Now for the coupled system according to law of conservation of momentum, total momentum of a system before and after collision remain conserved:

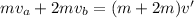`mv_(a) + 2mv_(b) = (m + 2m)v'` (1)

where,

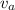`v_(a)` = velocity of the first car

`v_(b)` = velocity of the 2 coupled cars after collision

Now, from eqn (1)

`v' = (v_(a) + 2v_(b))/(3)`

`v' = \frac{3.00 + 2* 1.20}}{3}`

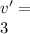
v' = 1.80 m/s

Therefore, the velocity of the combined car system after collision is 1.80 m/s