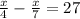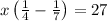Question

Amy drove to the mountains last weekend. There was heavy traffic on the way there, and the trip took 7 hours. When Amy drove home, there was no traffic and the trip only took 4 hours. If her average rate was 27 miles per hour faster on the trip home, how far away does Amy live from the mountains?

Answer 1

252 miles

Step-by-step explanation:

We define of the equation of the Velocity:

`V=d/t`

V: velocity (miles/hour)

d : distance(miles)

t: time (hours)

V1= Speed going to the montain= d/7

V2= Speed back home= d/4

Because the average rate was 27 miles per hour faster on the trip home:

`V2=V1+27`

`d/4=d/7+27`

`d/4-d/7=27`

(
`(7d-4d)/28=27`

`3d=28*27`

`d=756/3`

`d=252 miles`

Answer 2

Answer:252 miles

Step-by-step explanation:

Given

Amy took 7 hours while going

and it took only 4 hours on her return trip

Let
`v_g` be the average speed while going and
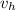`v_h` is the average speed while returning.

x is the distance between the home and mountain

therefore

`(x)/(4)-(x)/(7)=27`

`x\left ( (1)/(4)-(1)/(7)\right )=27`

`x=9* 4* 7=252 miles`