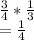Question

An urn contains 2 ​one-dollar bills, 1​ five-dollar bill and 1​ ten-dollar bill. A player draws bills one at a time without replacement from the urn until a​ ten-dollar bill is drawn. Then the game stops. All bills are kept by the player.​ Determine: ​(A) The probability of winning ​$15. ​(B) The probability of winning all bills in the urn. ​(C) The probability of the game stopping at the second draw.

Answer 1

Explanation:

Given that an urn contains 2 ​one-dollar bills, 1​ five-dollar bill and 1​ ten-dollar bill. A player draws bills one at a time without replacement from the urn until a​ ten-dollar bill is drawn.

The 10 dollar bill can be drawn either in I draw or II draw or III draw.

A) Prob of drawing 15 = Prob of drawing 5 in I draw and 10 in II draw

`(1)/(4) *(1)/(3) =(1)/(12)`

B) The probability of winning all bills in the urn.=Prob of drawing 10 dollar bill in IV draw = Prob of drawing one or 5 dollar in first three draws and last draw 10 dollar

=
`(2)/(4) *(1)/(3) *(1)/(2) +(1)/(4)* (2)/(3)* (1)/(2 ) \\\\=(1)/(6)`

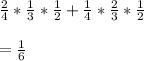
C) Prob of game stopping at second drawn = Prob of I draw non 10 and second draw 10

=
`(3)/(4)* (1)/(3) \\=(1)/(4)`