Answer: 3.49
Explanation:
When standard deviation is known then the test statistic for difference of two population means (independent population) is given by :-
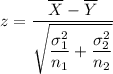
Given :
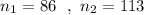
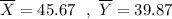
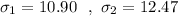
Then , the value of the test statistic will be :-
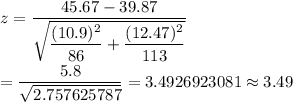
Hence, the value of the test statistic = 3.49