Answer: 896
Explanation:
Given The prior estimate of proportion of the population stay informed on local issues through the radio:
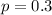
Margin of error :
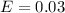
Significance level :
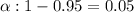
Critical value :
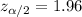
The formula to find the sample size :-
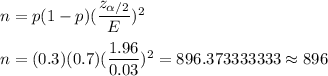
Hence, the necessary sample size is at least 896 .