Question

A baseball pitcher throws the ball in a motion where there is rotation of the forearm about the elbow joint as well as other movements. If the linear velocity of the ball relative to the elbow joint is 19.9 m/s at a distance of 0.490 m from the joint and the moment of inertia of the forearm is 0.500 kg·m2, what is the rotational kinetic energy of the forearm

Answer 1

Rotational kinetic energy of the forearm is 412.33 J.

Step-by-step explanation:

It is given that,

The linear velocity of the ball relative to the elbow joint is, v = 19.9 m/s

Distance from the joint, r = 0.49 m

Moment of inertia of the forearm, I = 0.5 kg/m²

We need to find the rotational kinetic energy of the forearm. It is given by :

`E=(1)/(2)I\omega^2`

`\omega` is the angular speed,
`\omega=(v)/(r)`

`E=(1)/(2)* 0.5\ kg/m^2* ((19.9\ m/s)/(0.49\ m))^2`

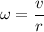
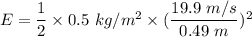
E = 412.33 J

So, the rotational kinetic energy of the forearm is 412.33 J. Hence this is the required solution.