Answer with explanation:
Given : A standardized exam's scores are normally distributed.
Mean test score :
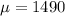
Standard deviation :
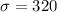
Let x be the random variable that represents the scores of students .
z-score :

We know that generally , z-scores lower than -1.96 or higher than 1.96 are considered unusual .
For x= 1900
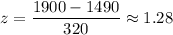
Since it lies between -1.96 and 1.96 , thus it is not unusual.
For x= 1240
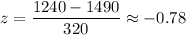
Since it lies between -1.96 and 1.96 , thus it is not unusual.
For x= 2190
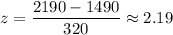
Since it is greater than 1.96 , thus it is unusual.
For x= 1240
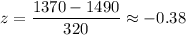
Since it lies between -1.96 and 1.96 , thus it is not unusual.