Question

A 47000 kg iceberg at −9.1 ◦C breaks away from the polar ice shelf and floats away into the ocean at 6.85◦C. What is the final change in the entropy of the system, when the iceberg has completely melted? The specific heat of ice is 2010 J/kg · ◦C. Answer in units of J/K.

Answer 1

Step-by-step explanation:

As it is known that relation between heat and specific heat is as follows.

Q =
`mC \Delta T`

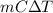
Heat evolved during phase change for temperature
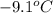`-9.1^(o)C` to
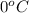`0 ^(o)C` is as follows.

Q =
`mC \Delta T`

=
`47000 kg * 2010 J/kg ^(o)C  * (0 - (-9.1))^(o)C`

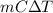
= 859677000 J ............ (1)

Heat evolved during phase change for temperature
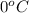`0 ^(o)C` to
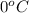`0 ^(o)C` is as follows.

Q =
`mC \Delta T`

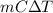
As temperature remains constant so, heat released will be equal to Q = m × l. Where l is latent heat of fusion on water equals 334 J/g.

Q = m × l

=
`47000 kg * 334 J/g (1000 g)/(1 kg)`

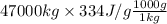
= 15698000000 J ........... (2)

Heat evolved during phase change for temperature
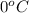`0 ^(o)C` to
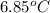`6.85 ^(o)C` is as follows.

Q =
`mC \Delta T`

=
`47000 kg * 2010 J/kg ^(o)C * (0 - 6.85)^(o)C`

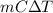
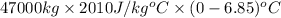
= 647119500 J .......... (3)

Now, total heat will be the sum of equations (1) + (2) + (3) as follows.

859677000 J + 15698000000 J + 647119500 J

= 17204796500 J

Also, relation between entropy and heat is as follows.

`\Delta S = (Q)/(\Delta T)`

=
`(17204796500 J)/(288.95 K)`

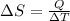
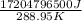
= 59542469.28 J/K

Thus, we can conclude that final change in entropy is 59542469.28 J/K.