Question

Which function has no horizontal asymptote?

A) f(x)=2x-1/3x2

B) f(x)=x-1/3x

C) f(x)=2x2/3x-1

D) f(x)=3x2/x2-1

Answer 1

C

Explanation:

Edge 2020-2021

Answer 2

Answer: Option C

C)
`f(x)=(2x^2)/(3x-1)`

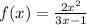
Explanation:

The horizontal asymptote is a line of the form:

`y = b`

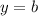
where b is a constant.

The horizontal asymptote is calculated by the following limit:

`y= \lim_(x \to \infty)f(x)`

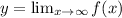
There is a simple way to know if a function has a horizontal asymptote, without calculating the limit

If f(x) is a function composed of division of polynomials of the form:

`f(x)=(ax^n+bx^(n-1)+c)/(ax^m+bx^(m-1)+c)`

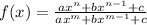
Then it is fulfilled that if the degree of the polynomial that is in the denominator is greater than or equal to the degree of the polynomial that is in the numerator then the function has a horizontal asymptote

This is:

If
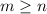`m\geq n` then then the function has a horizontal asymptote

Note that the only function that does not meet this condition is option C. Where n = 2 and m = 1.
`n>m`

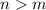
Then the answer is the option C