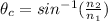Question

An example of when total internal reflection occurs is when all the light passing from a region of higher index of refraction to a region of lower index of refraction

passes through the region of lower index without being affected

passes through the region of lower index but is dispersed

is reflected back into the region of higher index

slows down so that objects appear bent

Answer 1

is reflected back into the region of higher index

Step-by-step explanation:

i js did the question

Answer 2

is reflected back into the region of higher index

Step-by-step explanation:

Total internal reflection is a phenomenon that occurs when all the light passing from a region of higher index of refraction to a region of lower index is reflected back into the region of higher index.

According to Snell's law, refraction of ligth is described by the equation

`n_1 sin \theta_1 = n_2 sin \theta_2`

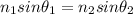
where

n1 is the refractive index of the first medium

n2 is the refractive index of the second medium

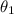`\theta_1` is the angle of incidence (in the first medium)

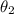`\theta_2` is the angle of refraction (in the second medium)

Let's now consider a situation in which

`n_1 > n_2`

so light is moving from a medium with higher index to a medium with lower index. We can re-write the equation as

`sin \theta_2 = (n_1)/(n_2)sin \theta_1`

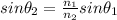
Where
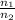`(n_1)/(n_2)` is a number greater than 1. This means that above a certain value of the angle of incidence
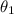`\theta_1`, the term on the right can become greater than 1. So this would mean

`sin \theta_2 > 1`

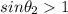
But this is not possible (the sine cannot be larger than 1), so no refraction occurs in this case, and all the light is reflected back into the initial medium (total internal reflection). The value of the angle of incidence above which this phenomen occurs is called critical angle, and it is given by

`\theta_c =sin^(-1)((n_2)/(n_1))`