Question

Here we go again lol I’m a failure and a disappointment according to my mom yayy

Answer 1

Hello! Your answer is y = -7/3x + 2.

----

First, find the slope of the original line. The slope can be calculated by
`(y_(2)-y_(1))/(x_(2)-x_(1))`. Substitute in the points, and you get:

`(3-(-3))/(13-(-1))`

`(6)/(14)`

`(3)/(7)`

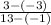
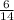
So now we get: slope = 3/7. We do not need the full equation of the first line, as a perpendicular line only requires the slope.

----

Perpendicular lines all have a slope that is a negative reciprocal of another. For example, if one line's slope was 1/4, the line perpendicular to it would have a slope of -4.

The negative reciprocal of 3/7 is -7/3. Therefore, we know the slope of the line that we are looking for is -7/3. We can substitute this into y = mx + b.

y = -7/3x + b

Now, we are given a coordinate point. Substitute that in and solve.

-5 = -7/3 * 3 + b

-5 = -7 + b

b = 2

----

Therefore, the final equation we are looking for is y = -7/3x + 2.

Hope this helps!