Question

7k^2-16k+100=0 using completing the square ?

Answer 1

`7k^2-16k+100=0`

`7k^2-16k=-100`

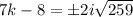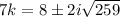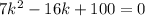
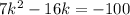
Add a squared constant to both sides:

`7k^2-16k+c^2=c^2-100`

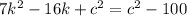
On the left, we wish to condense the quadratic into a squared binomial,

`(\sqrt7\,k-c)^2`

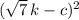
Expanding this gives

`7k^2-2c\sqrt7\,k+c^2`

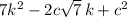
which tells us

`-2c\sqrt7=-16\implies c=\frac8{\sqrt7}`

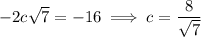
Then
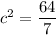`c^2=\frac{64}7`, and

`\left(\sqrt7\,k-\frac8{\sqrt7}\right)^2=\frac{64}7-100`

`\left(\sqrt7\,k-\frac8{\sqrt7}\right)^2=-\frac{636}7`

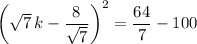
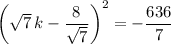
If you're looking for real-valued solutions, there are none, since the square root of a negative number doesn't exist... but if you're allowing complex-valued solutions, we can take the square root of both sides to get

`\sqrt7\,k-\frac8{\sqrt7}=\pm 2i\sqrt{\frac{259}7}`

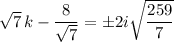
Multiply both sides by
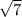`\sqrt 7` to eliminate denominators, then solve for
`k`:

`7k-8=\pm 2i√(259)`

`7k=8\pm 2i√(259)`

`\boxed{k=\frac{8\pm2i√(259)}7}`