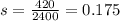Question

Quantities $r$ and $s$ vary inversely. When $r$ is $1200,$ $s$ is $0.35.$ What is the value of $s$ when $r$ is $2400$? Express your answer as a decimal to the nearest thousandths.

Answer 1

The value of s is 0.175.

Step-by-step explanation:

Given,

r and s vary inversely,

That is,

`r\propto (1)/(s)`

`\implies r=(k)/(s)`

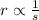
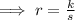
Where, k is the constant of proportionality,

We have, r = 1200 if s = 0.35,

`\implies 1200 = (k)/(0.35)`

`\implies k=1200* 0.35 = 420`

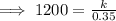
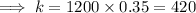
Thus, the equation that shows the relation between r and s is,

`r=(420)/(s)`

`\implies s=(420)/(r)`

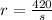
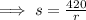
If r = 2400,

`s=(420)/(2400)=0.175`