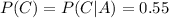Answer: Option D
Explanation:
First we assign names to events:
Event C: The selected people are from California
Event A: The selected person prefers the A mark
Now notice in the table that the total number of people is: 275.
Then, the number of people who prefer the A mark is: 176
The number of people who are from California is: 150
The number of people in California who prefer the A brand is: 96
Then we have that:
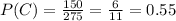
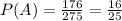
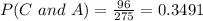
Then:
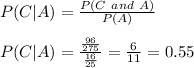
By definition two events C and A are independent if and only if:
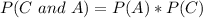
Then, if A and C are independent events, it must be fulfilled that:
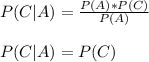
Note that
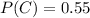 and
and
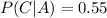
So:
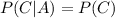
Therefore the events are independent and