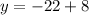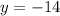Answer:

Explanation:
The formula for calculating the distance between two integers x and y is:
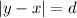
Where d is the difference between the two numbers and x is the smallest integer
In this case we know that
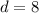 then:
then:
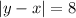
We also know that the product of both numbers is equal to 308.
This means that:
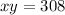
We know that
 and that
and that
 and
and

then the difference of
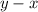 will always be positive, for this reason we can eliminate the absolute value of the first equation and we have that:
will always be positive, for this reason we can eliminate the absolute value of the first equation and we have that:
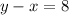
and
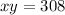
We substitute the first equation in the second equation:
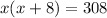
Now we solve for x:
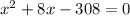
To factor the equation, you must look for two numbers that, by multiplying them, you get as a result -308 and by adding these numbers you get as a result 8.
These numbers are 22 and -14
Then the equation is as follows:
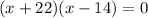
The solutions are:
 , and
, and

As we know that
 then we take the negative solution
then we take the negative solution

Finally we find the value of y.