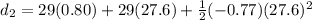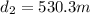Answer:
Part a)
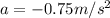
Part b)
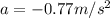
Part c)
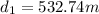
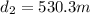
Step-by-step explanation:
Part a)
As we know that the relative speed of the two trains is given as
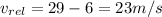
since the reaction time is 0.40 s
so the distance between two trains will reduce by

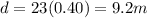
now we have the distance between them
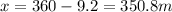
now the distance between them will become zero if the deceleration is "a"
now we have
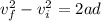
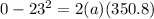
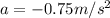
Part b)
If the reaction time is t = 0.80 s
so the distance between the two trains will be
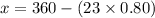
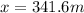
now we have
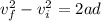
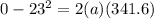
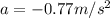
Part c)
Distance moved by the train in first case

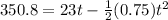
t = 28.4 s
now the distance
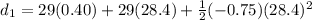
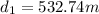
When reaction time is 0.8 s

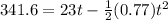
t = 27.6 s
now the distance