Question

Some basic properties of eigenvalues. Show the following: a) The eigenvalues of A and AT are the same. b) A is invertible if and only if A does not have a zero eigenvalue. c) If the eigenvalues of A are λ1, . . . , λn and A is invertible, then the eigenvalues of A−1 are 1/λ1, . . . , 1/λn. d) The eigenvalues of A and T −1AT are the same. Hint: you’ll need to use the facts that det A = det(AT), det(AB) = det A det B, and, if A is invertible, det A−1 = 1/ det A.

Answer 1

Explanation:

a) Since for any determinant we have

`|A|=|A^T|`

`|A- lemda I  |=0 then |A^T-lemda I |=0`

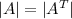
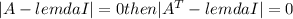
Hence both determinants would have the same eigen values

b) If A is having a zero value then by definition of eigen values we get

|A|=0. Hence we say if A is invertible if and only if A does not have a zero eigen value

c)
`|AA^(-1)|=1\\`

`|A^(-1) |=(1)/(|A|)`

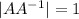
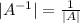
Hence eigen values of A would be the reciprocals of that of A transpose.