Question

A manufacturer of radial tires for automobiles has extensive data to support the fact that the lifetime of their tires follows a normal distribution with a mean of 42,100 miles and a standard deviation of 2,510 miles. Find the probability that a randomly selected tire will have a lifetime of between 44,500 miles and 48,000 miles. Be certain that you round your z-values to two decimal places. Round your answer to 4 decimal places.

Answer 1

Answer: 0.1591

Explanation:

Given : A manufacturer of radial tires for automobiles has extensive data to support the fact that the lifetime of their tires follows a normal distribution with

Mean :
`\mu=42,100\text{ miles}`

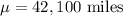
Standard deviation :
`\sigma=2,510\text{ miles}`

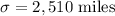
Let x be the random variable that represents the lifetime of the tires .

To find the probability that a randomly selected tire will have a lifetime of between 44,500 miles and 48,000 miles, we first the z-score corresponds to each value.

Formula for z-score :
`z=(x-\mu)/(\sigma)`

Now, For x= 44,500 miles

`z=(44500-42100)/(2510)\approx0.96`

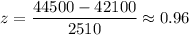
For x= 48,000 miles

`z=(48000-42100)/(2510)\approx2.35`

By using the standard normal distribution table , we have

The probability that a randomly selected tire will have a lifetime of between 44,500 miles and 48,000 miles
`=P(44500<x<48000)=P(0.96<z<2.35)`

`P(z<2.35)-P(z<0.96)= 0.9906132-0.8314724=0.1591408\approx0.1591`

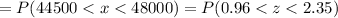
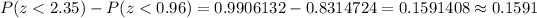
Hence, the probability that a randomly selected tire will have a lifetime of between 44,500 miles and 48,000 miles = 0.1591