Question

Choose the option that best answers the question.The points A(0, 0), B(0, 4a – 5) and C(2a + 1, 2a + 6) form a triangle. If Angle ABC = 90, what is the area of triangle ABC? 102 120 132 144 156

Answer 1

The correct option is 1.

Explanation:

Given information: The coordinates of a right angled triangle ABC are A(0, 0), B(0, 4a – 5) and C(2a + 1, 2a + 6). Angle ABC = 90°.

It means AB and BC are legs of the right angled triangle ABC.

Side AB lies on the y-axis because the x-coordinate of both A and B is 0.

Two legs are perpendicular to each other. So, BC must be parallel to x-axis and the y-coordinate of both B and C is must be same.

`4a-5=2a+6`

`4a-2a=5+6`

`2a=11`

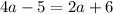
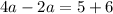
Divide both sides by 2.

`a=(11)/(2)`

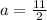
The value of a is 2. So the coordinates of triangle ABC are

`B(0,4a-5)=B(0,4((11)/(2))-5)\Rightarrow B(0,17)`

`C(2a+1,2a+6)=C(2((11)/(2))+1,2((11)/(2))+6)\Rightarrow C(12,17)`

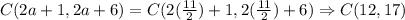
The area of a triangle is

`Area=(1)/(2)|x_1(y_2-y_3)+x_2(y_3-y_1)+x_3(y_1-y_2)|`

The area of triangle ABC is

`Area=(1)/(2)|0(17-17)+0(17-0)+12(0-17)|`

`Area=(1)/(2)|12(-17)|`

`Area=(1)/(2)|-204|`

`Area=(1)/(2)(204)`

`Area=102`

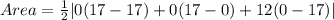
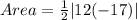
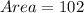
The area of triangle ABC is 102. Therefore the correct option is 1.