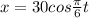Question

Ron is on a Ferris wheel of radius 30 ft that turns counterclockwise at a rate of one revolution every 12 seconds. The lowest point of the Ferris wheel​ (6 o'clock) is 15 feet above ground level at the point​ (0,15​) on a rectangular coordinate system. Find parametric equations of Ron as a function of time t​ (in seconds) if the Ferris wheel starts​ (t=​0) with Ron at the point ​(30​,45​).

Answer 1

`x = 30cos(\pi)/(6)t`

`y = 30sin(\pi)/(6)t + 45`

Step-by-step explanation:

1 full revolution is
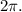`2\pi.` let \theta be the angle of Ron's position.

At t = 0.
`\theta = 0`

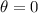
one full revolution occurs in 12 sec, so his angle at t time is

`\theta =2\pi (t)/(12) = (\pi)/(6)t`

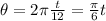
r is radius of circle and it is given as

`x = rcos\theta`

`y = rsin\theta`

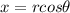
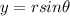
for r = 30 sec

`x = 30cos(\pi)/(6)t`

`y = 30sin(\pi)/(6)t`

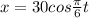
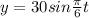
however, that is centered at (0,0) and the positioned at time t = 0 is (30,0). it is need to shift so that the start position is (30,45). it can be done by adding to y

`x = 30cos(\pi)/(6)t`

`y = 30sin(\pi)/(6)t + 45`