Question

Bill walks $\frac{1}{2}$ mile south, then $\frac{3}{4}$ mile east, and finally $\frac{1}{2}$ mile south. How many miles is he, in a direct line, from his starting point

Answer 1

1 1/4

Step-by-step explanation:

Find the length of the diagonal of the rectangle to find the length of the direct line to the starting time using Pythagorean Theorem.

1 1/4

heh, not a really good explanation but at least it's correct XD

Answer 2

Step-by-step explanation:

The attached figure shows the whole description.

Fraction covered in south,
`x_1=(1)/(2)`

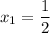
Fraction covered in east,
`x_2=(3)/(4)`

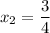
Fraction covered in south,
`x_3=(1)/(2)`

MNO is a right angle triangle.

`MO^2=MN^2+NO^2`

`MO^2=(3/8)^2+(1/2)^2`

`MO=0.62\ mile`

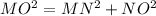
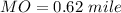
So,
`AM=2* MO`

`AM=2* 0.62`

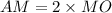
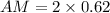
AM = 1.24 miles

So, he is 1.24 miles from his starting point. Hence, this is the required solution.