Question

What will be the final temperature of a 207.0 g piece of copper (specific heat = 0.385Jg∘C) that absorbs 5.00 kJ of heat starting at 80.4∘C? Report your answer with the correct number of significant figures.

Answer 1

The answer to your question is: T2 = 133.1°C

Step-by-step explanation:

Data

mass = 207 g

Cp = 0.385J/g°C

Q = 5 kJ = 5000 J

T1 = 80.4 °C

T2 = ?

Formula

Q = mCp(T2 - T1)

(T2 - T1) = Q / mCp

T2 = T1 + Q/mCp

Substitution

T2 = 80.4 + 5000/(207)(0.385)

T2 = 80.4 + 5000 / 79.7

T2 = 80.4 + 52.7

T2 = 133.1°C

Answer 2

Step-by-step explanation:

It is given that,

Mass of copper, m = 207 g

Specific heat of copper,
`c=0.385\ Jg^oC`

Heat absorbed,
`Q=5\ kJ=5000\ J`

Initial temperature,
`T_i=80.4^oC`

Let
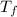`T_f` is the final temperature of copper. Heat absorbed is given by :

`Q=mc(T_f-T_i)`

`T_f=(Q)/(mc)+T_i`

`T_f=(5000)/(207* 0.385)+80.4`

`T_f=143.13^oC`

So, the final temperature of the copper is 143.13 degree Celsius. Hence, this is the required solution.