Question

Find a factorization of 2^6 +1 and 2^12+1 as a sum of two cubes

Answer 1

(4+1)(4^2 - 4*1+1)

(16+1)(16^2-16+1)

Explanation:

Sum of cubes is a common case of factorization:

`x^(3)+y^(3)=(x+y)(x^(2) -xy+y^(2) )`

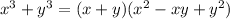
The first case can be written as: (2^2)^3+1^3= 4^3 + 1^3 which can be factorized as (4+1)(4^2 - 4*1+1)

And we can solve it, and the result is 65.

The second case can be written as (2^4)^3 + 1^3= (16^3 +1^3) which can be factorized as (16+1)(16^2-16+1)=(17)*(241)=4097