Question

A quantity with an initial value of 6200 decays continuously at a rate of 5.5% per month. What is the value of the quantity after 4 years, to the nearest hundredth?

Answer 1

442.44

Explanation:

Answer 2

410.32

Explanation:

Given that the initial quantity, Q= 6200

Decay rate, r = 5.5% per month

So, the value of quantity after 1 month,
`q_1 = Q- r * Q`

`q_1 = Q(1-r)\cdots(i)`

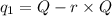
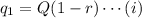
The value of quantity after 2 months,
`q_2 = q_1- r * q_1`

`q_2 = q_1(1-r)`

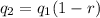
From equation (i)

`q_2=Q(1-r)(1-r) \\\\q_2=Q(1-r)^2\cdots(ii)`

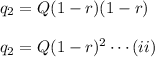
The value of quantity after 3 months,
`q_3 = q_2- r * q_2`

`q_3 = q_2(1-r)`

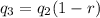
From equation (ii)

`q_3=Q(1-r)^2(1-r)`

`q_3=Q(1-r)^3`

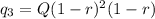
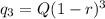
Similarly, the value of quantity after n months,

`q_n= Q(1- r)^n`

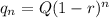
As 4 years = 48 months, so puttion n=48 to get the value of quantity after 4 years, we have,

`q_(48)=Q(1-r)^(48)`

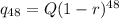
Putting Q=6200 and r=5.5%=0.055, we have

`q_(48)=6200(1-0.055)^(48) \\\\q_(48)=410.32`

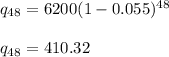
Hence, the value of quantity after 4 years is 410.32.