Answer:
C.
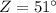
Explanation:
We have been given a triangle. We are asked to find the measure of angle Z using Law of cosines.
Law of cosines:
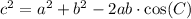 , where, a, b and c are sides opposite to angles A, B and C respectively.
, where, a, b and c are sides opposite to angles A, B and C respectively.
Upon substituting our given values in law of cosines, we will get:
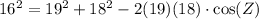
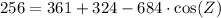
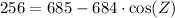
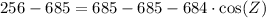
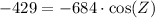
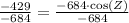
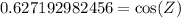
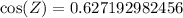
Now, we will use inverse cosine or arc-cos to solve for angle Z as:
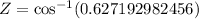
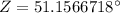
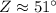
Therefore, the measure of angle Z is approximately 51 degrees.