Question

I need help to solve this and also Hearn will the bacteria be over 100,000

Answer 1

Hello! Let's look at the two parts of this question.

Complete the table:

In this case, you just substitute the value of "hour" into the equation, for the value of t. For example:

P(0) = 120
`(2)^(0)`

P(0) = 120 (1)

P(0) = 120

Therefore, the number of bacteria for hour 0 is 120.

You can do this for the next ones. Hour 1 = 240, hour 2 = 480, and so on. (In this case, you can keep multiplying by 2)

Estimate when there will be more than 100,000 bacteria:

Set the final value of P(t) = 100,000, then solve.

100,000 = 120 (2
`)^(t)`

833.33 = (2
`)^(t)`

t =
`log_(2)833.33`

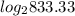
t = 9.702744108

So your answer would be around 9.7 years, or, around 10 years.

Hope this helps!