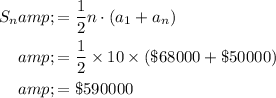Question

N. Creasing is starting a job with a starting annual salary of $50000. Each subsequent year her salary will increase $2000. What will her 10th year salary be? Write an expression in sigma notation showing her cumulative salary for the decade, and then evaluate the expression.​

Answer 1

$68,000.

Sum of salaries in the first ten years:

`\displaystyle \sum_(n = 1)^(10){(\$50000 + (n - 1)* \$2000)} = \$590000`.

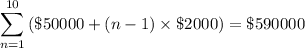Explanation:

Start by considering the salary for the first few years:

`\begin{array}c\text{Year}&\text{Salary}\\\cline{1-2}\\[-0.5em]\text{1st}& \$50000+0* \$2000\\\text{2nd}&\$50000 + 1*\$2000\\\text{3rd}&\$50000 + 2* \$2000\\\vdots&\vdots\\n\text{th}&\$50000 + (n - 1)* \$2000\end{array}`.

Observe the trend in annual salary. The salary on the nth year will be equal to
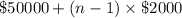`\$50000 + (n - 1)* \$2000`. The salary on the 10th year will thus be equal to

`\$50000+(10-1)* \$2000 = \$68000`.

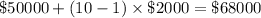The sum of the salaries for the first ten years will be:

`\displaystyle \sum_(n = 1)^(10){(\$50000 + (n - 1)* \$2000)}`.

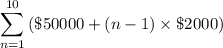This series is arithmetic:

`\begin{aligned}&\displaystyle \sum_(n = 1)^(10){(\$50000 + (n - 1)* \$2000)}\\=&\$50000 + \$52000 + \cdots + \$68000\end{aligned}`.

• First term:
  `a_1 = \$50000`;
• Last term:
  `\$68000`;
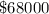• Number of terms:
  `10`.

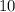Evaluate this expression using the formula for the sum of an arithmetic series:

`\begin{aligned}S_n &= (1)/(2) n \cdot (a_1 + a_n)\\&= (1)/(2) * 10 * (\$68000 + \$50000) \\&= \$590000\end{aligned}`