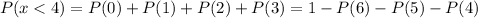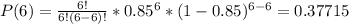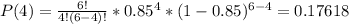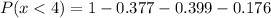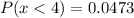Question

From experience an airline knows that only 85% passengers

booked for a certain fly actually show up if 6 passengers are randomly selected find the probability that fewer than four of them show up

Answer 1

`P(x<4) =0.0473`

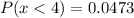
Explanation:

Let's call p the probability that a passenger shows up.

Then we know that:

`p = 0.85`

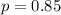
Then we took a sample of n = 6 passengers.

We can calculate the probability that less than 4 are presented using the binomial formula:

`P(x) = (n!)/(x!(n-x)!)*p^x*(1-p)^(n-x)`

Where x is the number of passengers that show up, n is the number of selected passengers, p is the probability that a passenger shows up.

Then we look for:

`P(x<4) = P(0) +P(1) +P(2) +P(3)=1-P(6)-P(5)-P(4)`

`P(6) = (6!)/(6!(6-6)!)*0.85^6*(1-0.85)^(6-6)=0.37715`

`P(5) = (6!)/(5!(6-5)!)*0.85^5*(1-0.85)^(6-5)=0.39933`

`P(4) = (6!)/(4!(6-4)!)*0.85^4*(1-0.85)^(6-4)=0.17618`

`P(x<4) =1-0.377-0.399-0.176`

`P(x<4) =0.0473`