Question

Fluoride ion is poisonous in relatively low amounts: 0.2 g of F- per 70 kg of body weight can cause death. Nevertheless, in order to prevent tooth decay, F- ions are added to drinking water at a concentration of 1 mg of F- ion per L of water. How many liters of fluoridated drinking water would a 70-kg person have to consume in one day to reach this toxic level? How many kilograms of sodium fluoride would be needed to treat a 8.5 x107-gal reservoir?

Answer 1

`\boxed{\text{(a) 14 L; (b) 711 kg}}`

Step-by-step explanation:

(a) Litres of water

`\text{Mass of F}^(-) = 8.5 * 10^(7)\text{ gal} * \frac{\text{0.2 mg F}^(-)}{\text{1 kg}} = \textbf{14 mg F}^(-)\\\\\text{Volume of water} = \text{14 mg F}^(-) * \frac{\text{1 L water}}{\text{1 mg F}^(-)} = \textbf{14 L water}\\\\\text{The person would have to consume $\boxed{\textbf{14 L}}$ of water per day}`

(b) Mass of NaF

`\text{Volume} =8.5 * 10^(7) \text{gal} * \frac{\text{3.785 L}}{\text{1 gal}} = 3.22 * 10^(8)\text{ L}\\\\\text{Milligrams of F}^(-) = 3.22 * 10^(8)\text{ L} * \frac{\text{ 1 mg F}^(-)}{\text{1 L}} = 3.22 * 10^(8)\text{ mg F}^(-)\\\\\text{kilograms of F}^(-) = 3.22 * 10^(8)\text{ mg F}^(-) * \frac{\text{1 mg F}^(-)}{10^(6)\text{kg F⁻}} = \text{322 kg F}^(-)`

1 kmol of NaF (41.99 kg) contains 19.00 kg of F⁻.

`\text{Kilograms of NaF}= \text{322 kg F}^(-) * \frac{\text{41.99 kg NaF}}{\text{19.00 kg F}^(-)} = \text{711 kg NaF}\\\\\text{It will take } \boxed{\textbf{711 kg}} \text{ of NaF to treat the reservoir}`

Answer 2

Step-by-step explanation:

(a) The given data is as follows.

Concentration = 1 mg/L, Toxic amount = 0.2 g

Now, we will calculate the volume of fluoridated drinking water as follows.

`V_((water, toxic)) = \frac{\text{toxic amount}}{\text{concentration}}`

=
`(0.2 g)/(10^(-3) g/L)`

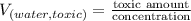
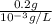
= 200 L

Hence, there will be 200 liters of fluoridated drinking water would a 70-kg person have to consume in one day to reach this toxic level.

(b) Now, it is also given that

V =
`850 * 10^(7) gal`

We will convert gallons into liters as follows.

`850 * 10^(7) gal * 3785 L/gal`

=
`32183 * 10^(8) L`

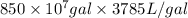
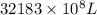
Concentration = 1 mg/L

Therefore, we will calculate the mass as follows.

m =
`\text{volume * concentration}`
`\text{volume} * \text{concentration}`

=
`32183 * 10^(8) * 1 mg/L`

=
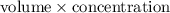
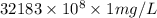
`32183 * 10^(2) kg` (As 1 mg =
`10^(-6)` kg)

Thus, we can conclude that there are
`32183 * 10^(2) kg` of sodium fluoride would be needed to treat a
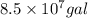`8.5 * 10^(7) gal` reservoir.