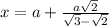Question

A charge 3q is at the origin, and a charge −2q is on the positive x axis at x=a. part a where on the x-axis would you place a third charge so it would experience no net electric force? enter an expression for the exact answer, which will involve a square-root sign. (do not enter an approximate decimal answer.)

Answer 1

`x = a + (a\sqrt2)/(\sqrt3 - \sqrt2)`

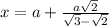
Step-by-step explanation:

Position of charge 3q is x = 0

position of charge -2q is x = a

so here we know that

when two charges are of opposite nature then the electric field will be zero on the line joining the two charges at the position near to smaller magnitude charge

So here the electric field will be zero if the field due to 3q is counterbalanced by field due to -2q

so here we can say

`(k(3q))/((r+a)^2) + (k(-2q))/(r^2) = 0`

`(3)/((r + a)^2) = (2)/(r^2)`

`(r+a)/(r) = \sqrt{(3)/(2)}`

`1 + (a)/(r) =\sqrt{(3)/(2)}`

`(a)/(r) = (\sqrt3 - \sqrt2)/(\sqrt2)`

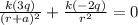
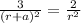
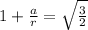
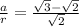
so we will have

`r = (a\sqrt2)/(\sqrt3 - \sqrt2)`

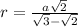
so the x coordinate of this position is given as

`x = a + (a\sqrt2)/(\sqrt3 - \sqrt2)`