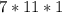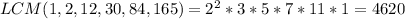Question

Lcm of 1,2,12,30,84,165

Answer 1

`LCM(1,2,12,30,84,165)=2^2*3*5*7*11*1=4620`

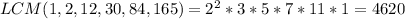
Explanation:

To find the LCM of 1,2,12,30,84,165 you must first find the prime factors of 12,30,84 and 165

12| 2 30| 2 84| 2 165| 3

6 | 2 15 | 3 42| 2 55 | 5

3 | 3 5 | 5 21 | 3 11 | 11

1 1 7 | 7 1

1

`12=2^2*3`
`30=2*3*5`
`84=2^2*3*7`
`165=3*5*11`

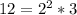
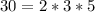
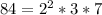
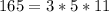
Now we look for common and uncommon factors with their greatest exponent

LCM(1,2,12,30,84,165)

Common factors with their greatest exponent:
`2^2*3*5`

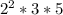
Uncommon factors with their greatest exponent:
`7*11*1`

`LCM(1,2,12,30,84,165)=2^2*3*5*7*11*1=4620`