Answer:
exit velocity = 62 m/s
exit pressure is 98.52332 kPa
Step-by-step explanation:
given data
pressure p1 = 80 kPa
temperature t1 = 27°C = 300 K
velocity v1 = 220 m/s
temperature t2 = 42°C = 315K
area exit = 370 cm²
lose heat at a rate = 18 kJ/s
gas constant of air = 0.287 kPa·m^3/kg·K.
h1 = 300.19 kJ/kg
h2 = 315.27 kJ/kg
to find out
exit velocity and exit pressure
solution
first we apply here energy balance equation to find out outlet velocity
Einlet = Eoutlet
m(h1 + v1²/2) = m (h2+v2²/2) +Q
m(v1²-v2²) /2 = m (h2 -h1) +Q
v2² = v1² - 2Cp Δt - 2Q/m
here Δt = h2 - h1 and put all value
v2² = 220² - 2(1.005)10³ (15) - 2(18)10³ /2.5
exit velocity = 62 m/s
so
now find outlet pressure that is
p2 = mRT / A2 v2
put value
p2 = 2.5 (287) 315 / (370
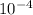 62)
62)
p2 = 98.52332 kPa
exit pressure is 98.52332 kPa