Question

Let a and b be real constants such that \[x^4 ax^3 3x^2 bx 1 \ge 0\]for all real numbers x. Find the largest possible value of a^2 b^2.

Answer 1

Infinity

Explanation:

Since
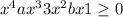`x^4 ax^3 3x^2 bx 1 \ge 0` for all real numbers x, this property is also true for x=1, which tells us that

`1^4 a1^3 3\cdot1^2 b\cdot 1=3ab\ge0`

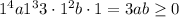
On the other hand, note that for all real numbers x, it holds that

`x^4x^3x^2x\ge 0`

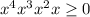
Therefore, if

`3ab\geq0`

we have tat

`3ab x^(4)x^(3)x^(2)x^(1)1=x^4ax^3 3x^2bx1\ge0`

The last reasoning tells us that the property
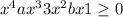`x^4 ax^3 3x^2 bx 1 \ge 0` holds for all real numbers x if an only if
`ab\ge0`

Therefore, we can choose arbitrary constants a and b as long as

`ab\ge0`

We can choose a and b such that both positive, both negative or one of the two constants is equal two zero. In the first two cases

`a^2b^2`

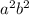
can get as big as we want, depending on the constants, and we are done.